Matematik karar vermenize nasıl yardımcı olur?

Sergey Bobrovsky, Airbus'ta Yapay Zeka Platformlarında Veri Bilimcisi ve Veri Bilimi için Matematik ve İstatistik kursumuzun eğitmenidir. Webinarda Sergey, hangi matematik yaklaşımlarının var olduğunu, bu bilimin hayatta bize nasıl yardımcı olduğunu ve "siyah kuğu" nun ne anlama geldiğini anlatacaktır. Özetini burada sizlerle paylaşmak istiyoruz.

Matematik Nedir?
 

Matematik nedir? Bu felsefi sorunun basit bir yanıtı yok. Dört temel kavramı vardır:

#1. Matematik Farklı Bir Dünyadır

#2. Matematik Mantıktır

#3. Matematik, Matematikçilerin Kendileri Tarafından Yaratılan Bir Yapıdır.

#4. Matematik Bir Oyundur

Başka Bir Dünya

İlk kavram, filozof Platon'un görüşüdür. Matematikçilerin başka bir dünyayı, fikirlerin dünyasını keşfettiklerine inanıyordu. Bir teoremi ispatladığımızda öncü gibi davranıyoruz çünkü bu bir matematik dünyasıdır.

Uzun zaman boyunca insanların, kendilerinin başka dünyalara kapı açtığına dair bir inancı olmuştur.

Mantık

XIX-XX yüzyılların eğilimi, Platonculuktan ayrılmak olmuştu. Biçimsel mantığın gelişmesiyle bilim adamları, aslında matematiğin rasyonel düşünme olduğu sonucuna vardılar.

Diğer İfadelerin Nasıl Çıkarılabileceğinin İncelenmesi Mantık ile İlişkilidir. Bu Yaklaşımın Kurucularından Biri Bertrand Russell'dı.

Biçimsel mantık, öncüller doğruysa son ifadenin de doğru olacağını garanti eder.

Ancak zamanla her şeyin o kadar basit olmadığı ortaya çıktı.

Russell öncüllerin doğruluğunun, sonuçların doğruluğunu garanti ettiğine inanıyordu. Matematiğin tüm basit aksiyomlarını bulabilirsek, tüm sonuçları mantığın yardımıyla çıkarabiliriz. Aslında, tüm teoremlerin aksiyomlar temelinde inşa edilemeyeceği ortaya çıktı.

Yapısı

Russell okulunun muhalifleri sezgicilerdi (Profesör Friedrich Bauer'in takipçileri).

Platoncular, matematikçilerin kendileri olmadan var olan bir dünyayı keşfettiklerine inanıyorlarsa, o zaman sezgiciliğin taraftarları, matematikçilerin sonuçlarını kendilerinin oluşturduğunu düşünürler. Böylece, aksiyomlara dayalı doğru sonuçları kendimiz yaratırız ve matematik sadece bir yapı olarak kalır.

Oyun

Önde gelen matematikçilerden biri olan David Hilbert, matematiğin oldukça zor bir oyun olduğuna inanıyordu. Matematikçiler, sembollerle çalışan (masa oyunlarında olduğu gibi) belirli kurallara göre oynarlar. Yalnızca temel aritmetiğin (parmaklarımızla sayılan) doğrudan bir anlamı vardır. Geri kalan her şey kendi içinde kapalı bir oyun sistemidir. Kurallara göre oynarsanız, her zaman ilginç sonuçlarla karşılaşacaksınız. Ama istediğinizi yapmakta özgürsünüz. Bu nedenle, matematik felsefesine yatırım yapmaya gerek yok. Matematik sadece kurallarını kendimizin icat ettiği bir oyundur.

Matematik Neden Önemlidir?
 

Matematik her yerdedir! Şimdiye kadar kaydettiğimiz tüm ilerleme, matematiği kullanmaya başladığımız için mümkün oldu.

Amerikalı fizikçi Eugene Wigner, “Matematiğin Doğa Bilimlerinde Anlaşılmaz Etkililiği” adlı makalesinde, bazı yazılı formüllerin dünyada olup bitenleri neden gerçekten etkilediğini anlamaya çalıştı. Ancak bu sorunun evrensel bir yanıtı yok.

Matematik, ilişkilerimizi nasıl modellediğimizi gösterir. Örneğin:

Kendinize sıcak kahve yaptınız ve süt eklemek istediniz ama biri sizi telefonla aradı ve kahvenizi hemen içmediniz.

Soru: Kahveye süt eklemek ne zaman daha mantıklıdır: hemen mi yoksa içmeden önce mi?

Matematiksel olarak açıklayalım. Herhangi bir andaki kahvenin sıcaklığıyla ilgileniyoruz. Soğumanın sıcaklık farkına bağlı olduğunu gözlemliyoruz. Yani, oda sıcaklığındaki bir sıvıyı masanın üzerinde bırakırsanız neredeyse soğumaz. Sıcak şeyler çok çabuk soğur.

Sıcaklığın zamana göre değişiminin diferansiyel denklemini yapalım. Bu denklemi çözmek üstel soğumaya yol açar.

Yani, kahvenin herhangi bir andaki sıcaklığı başlangıç sıcaklığı ile ortam sıcaklığı arasındaki farktır ve bu sıcaklık zamanla katlanarak düşer. t sonsuza yaklaştıkça kahve oda sıcaklığına gelir.

Baştan süt eklersem kahvenin karışma anında sıcaklığı düşüyor, 32.5 dereceye ulaşmış oluyor. Süt hemen eklenmeden bekletilirse, 20 derece sıcaklığında bir kahve içmiş olurum.

Sonuç: Soğuk kahve içmek istemiyorsanız, hemen süt eklemeniz gerekiyor.

Bilinen Düşünce Hataları
 

Bilincimizin sorunlarından biri, olasılığı şu ya da bu sonuca atanan bir tür değişmeyen sabit olarak algılamamızdır. Aslında olasılığı, yeni gerçekler öğrendikçe değişebilen bir olaya duyulan güvenin derecesi olarak düşünmek daha mantıklıdır.

• Kurtulanın Hatası

İkinci Dünya Savaşı sırasında uçağın hangi kısmının zırhla güçlendirileceğine karar verdiklerinde, kaza yapmayan veya yok edilmeyen uçakların hangi yerlerinin en çok mermilerle vurulduğunu araştırdılar.

Ancak, deliklerin güçlendirilmesi gereken yerlerde değil, uçağa en az zarar verecek yerlerde olduğu ortaya çıktı. Bu nedenle, uçağın isabet almayan kısımlarını ayırmanız gerekiyor. Çünkü delik olan tüm uçaklar bu "beyaz" bölgelerde düştü.

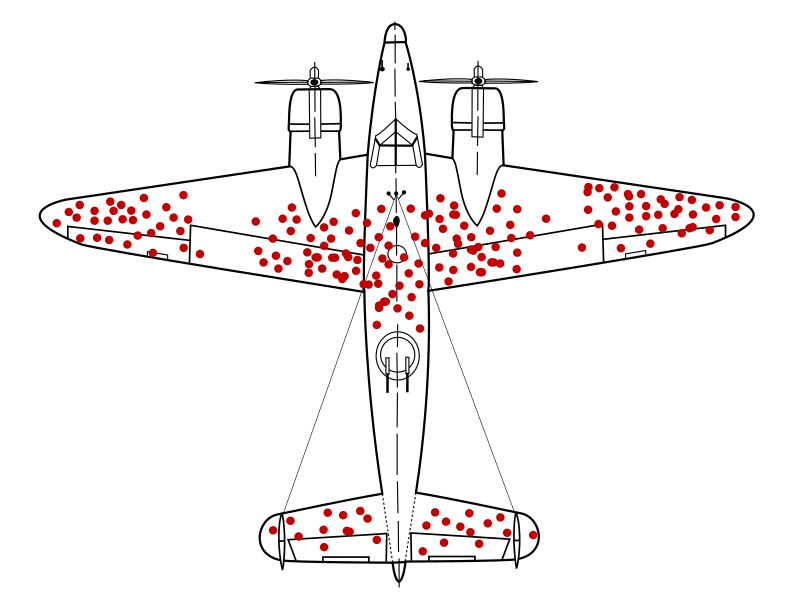
Yani kararlarımızı "hayatta kalanlardan" alınan verilere dayandırırsak, "ölüler" hakkında yeterli bilgiye sahip olmadığımız için yanlış sonuçlara varabiliriz. Örneğin, ünlülerin hikayelerini biliyoruz ve başarılı olmak için onlar gibi davranmamız gerektiğini düşünüyoruz. Ancak başarılı insanlarla aynı şeyleri yapan ama hiçbir şey elde edemeyen birçok insan mevcut ve onlar hakkında yeterince bilgi sahibi değiliz. Sadece kazananların yolunu takip ediyoruz.

• Oyuncu Hatası

Rulet oynarken arka arkaya birçok kez kırmızı düşerse, o zaman kumarhane ziyaretçisi siyah olasılığının arttığını (ve ya tam tersi) düşünür. Ama aslında öyle değildir.

Monte Carlo'da top arka arkaya 26 kez siyah geldi ve sonuç olarak oyuncular çok para kaybetti çünkü 10 atıştan sonra kırmızının düşeceğinden eminlerdi.

• Temel Yüzde Hatası

2,8 milyon insan için 100 terörist varsa ve onları aramak için vakaların %1'inde yanlış olan bir sistem varsa, o zaman sistem alarm verdiğinde vakaların sadece %0,3'ünde gösterdiği kişi gerçekten bir terörist olacaktır. %1 hata çok az gibi görünse de bu, sistemin doğru olması gerektiği anlamına gelir. Hastalık testlerinde de durum aynıdır - doğruluklar aslında hastalıkların yaygınlığına bağlıdır.

Verilen örneklerin çoğu Nobel ödüllü Daniel Kahneman'ın "Yavaş Düşün, Hızlı Karar Ver" kitabından alınmıştır. İki karar sistemimiz olduğunu söylüyor. Biri hızlı ve otomatik ve onu kullanmak için zorlanmak zorunda değiliz. İkincisi ise tam tersine konsantre olmanız, hesap yapmanız ve çaba göstermeniz gerektiren bir sistemdir. Çoğu zaman, 2. sistemi kullandığımızı sandığımızda aslında 1. sistemi kullanıyoruz çünkü enerji, dikkat ve zamandan tasarruf ediyoruz. Bu genellikle doğru bir yaklaşımdır ve çevremizdeki tehlikelere hızla yanıt vermemizi sağlar.

Ancak günümüz dünyasında, özellikle finansal riskler söz konusu olduğunda, tehlikelerin çoğu daha karmaşık bir yapıya sahiptir.

Kayıp sorununu, parasal kayıplarla ilişkilendirildiğinde çözmek çok daha kolaydır. Ancak kayıpları psikoloji ile ilişkilendirirsek, psikolojimizin tamamen rasyonel olmadığı ortaya çıkar ve kazançlara sevinmekten çok kayıplardan korkarız. Bu nedenle, genellikle kazançları en üst düzeye çıkarmak yerine kayıpları en aza indirmeye çalışırız. Yani her seferinde 10$ kaybetmek bizim için bir kez 100$ kazanmaktan daha zordur.

Kendi risk politikanızı belirlemeniz tavsiye edilir. Ortalama olarak ne kadar kayıpla yaşayabileceğinize önceden karar verin ve her zaman bu politikayı kullanın. Örneğin, ek sigorta satın almayın. Ortalama kazançlara bakmaya çalışan, hisse senedi tüccarları gibi düşünmek her zaman daha iyidir. Önemli olan yeterince sık kazanmaktır ama bazen kaybetmek iyidir.

Tavsiye etmek istediğim ikinci kitap, Nassim Taleb'in "Kara Kuğu" kitabıdır. Okursanız, burada bahsettiğim şey ile çelişiyor gibi görünebilir. Çünkü matematiğin aşırı kullanımı olaylar üzerinde kontrol yanılsamasına yol açar.

Bir hindinin bir çiftlikte yaşadığını, her gün lezzetli yiyeceklerle beslendiğini ve bu bilgilere dayanarak gelecekte ne kadar yiyecek alacağını hesapladığını düşünün. Ancak Şükran Günü'nün yakında geleceğini hesaba katmaz, bu da katledileceği anlamına gelir.

Yani, tüm teorilerin kendi kapsamları ve ön koşulları vardır. Nadiren beklemediğimiz olaylar da oluyor. Bu nedenle matematiği çok dikkatli uygulamalıyız ve ne zaman işe yarayıp ne zaman yaramadığını anlamalıyız.

Gösterilen örneklerin çoğu basit oyun örnekleridir. Bizi doğru düşünceden uzaklaştırabilirler. Her zaman öğrendiğimiz belirli kurallara göre düşünmeliyiz. Olasılık kavramı, değişebilecek bir olaya olan güven derecesi olarak ele alınmalıdır ancak o zaman olasılık teorisi karar vermede yardımcı olacaktır.

Matematiğin Karar Vermede Nasıl Kullanılır?
 

• Olasılıkları içeren kararlar alırken çok dikkatli olun. Vücudumuz hızlı ama genellikle yanlış kararlar önerebilir.
• Acele etmeyin ve durumu analiz edin. Matematiği kullanın, Bayes teoremi bu konuda size yardımcı olacaktır.
• Olasılıkları bir durumu bilme ya da bilmeme dereceleri olarak düşünün. Yeni bilgiler alındıktan sonra olasılıklar değişebilir.
• Küçük örneklemlerden genelleme yapmayın. Beş kişiden oluşan bir örneğiniz varsa, bunu tüm popülasyona yaymayın.
• Hangi risk düzeyinde rahat olduğunuza karar verin ve her zaman buna bağlı kalın.
• Bazen nadir olayların bile olduğunu unutmayın.