Simpson Paradoksu: Veri Yanılgılarını Anlamak

"Paradoks" terimi, Yunanca "paradoxon" kelimesinden türemiştir ve akılla çelişen ya da ona karşı gelen bir şeyi ifade eder. Paradokslar, genellikle mantık ve felsefenin kesiştiği noktada ortaya çıkan, insan zekasının harikalarıdır. Günümüzde, istatistik biliminin en büyüleyici ve önemli paradokslarından biri Simpson Paradoksu’dur ve bu paradoks, tıbbi araştırma, data analizi ve çeşitli uygulama alanları için anlamlı ifadeler taşır.

1951'de Simpson, çeşitli alt gruplar veya bireylerden oluşan geniş bir popülasyon içinde gözlemlenen bir istatistiksel ilişkinin, bu popülasyonu oluşturan her bir alt grup içinde tersine dönebileceğini ve farklı sonuçlar yansıtabileceğini göstermiştir. Bu görünür paradoks, tıp ve sosyal bilimler için önemli sonuçlar doğurur: Popülasyon düzeyinde etkili görünen bir tedavi, aslında popülasyonun her bir alt grubu içinde zararlı sonuçlara yol açabilir. Örneğin, daha yüksek bir ilaç dozu, genel olarak daha yüksek iyileşme oranlarıyla ilişkilendirilirken, alt gruplar içinde (örneğin, her iki cinsiyet için) daha yüksek doz, aslında daha düşük iyileşme oranlarına neden olabilir. Simpson Paradoksu, göz ardı edilen karıştırıcı değişkenler ve bu değişkenlerin dengesiz dağılımı ile ilişkili olması nedeniyle özellikle ilgi çekicidir.

Simpson Paradoksu’na Grafiksel Bir Bakış

Simpson Paradoksu, esas olarak, incelenen iki ana değişken arasındaki ilişkiyi etkileyen üçüncü bir eleman olan bir karıştırıcı değişkenin varlığı nedeniyle ortaya çıkar. Bu karıştırıcı değişken dikkate alınmadığında, veri ilişkilerinin yanlış yorumlanmasına yol açabilir. Paradoks genellikle, veri birleştirme sürecinde bu karıştırıcıların etkisinin göz ardı edilmesiyle ortaya çıkar ve araştırmacıların değişkenler arasındaki gerçek ilişkinin doğasını kaçırmasına neden olur.

Bu fenomen, regresyon analizindeki eksik değişken yanlılığı kavramını yansıtır. Burada kritik alt grup bilgileri veya karıştırıcılar analize dahil edilmediğinde analiz sonucu bozulabilir. Potansiyel karıştırıcı değişkenleri anlamak ve tanımlamak, doğru yorumlar sağlamak için herhangi bir istatistiksel analizde temel adımlardır.

Paradoksu grafiksel olarak incelemek, paradoksun doğasını açıklığa kavuşturur. Başlangıç analizinin iki değişken, X ve Y arasında negatif bir korelasyon gösterdiği bir senaryoyu düşünün: X arttıkça Y azalır. Ancak, alt grup analizi denkleme dahil edildiğinde, X ve Y arasında aslında pozitif bir korelasyon olduğu ortaya çıkar ve başlangıçtaki gözlemle çelişir. Bu örnek, alt grup ayrımlarının göz ardı edilmesinin değişkenler arasındaki gerçek ilişkiyi nasıl bulanıklaştırabileceğini gösterir.

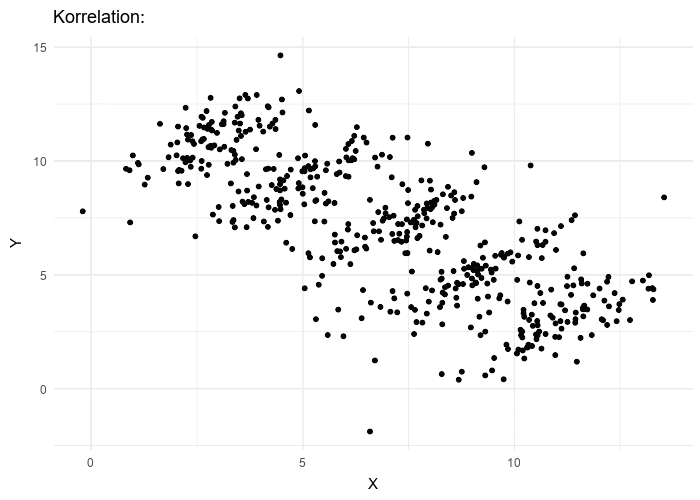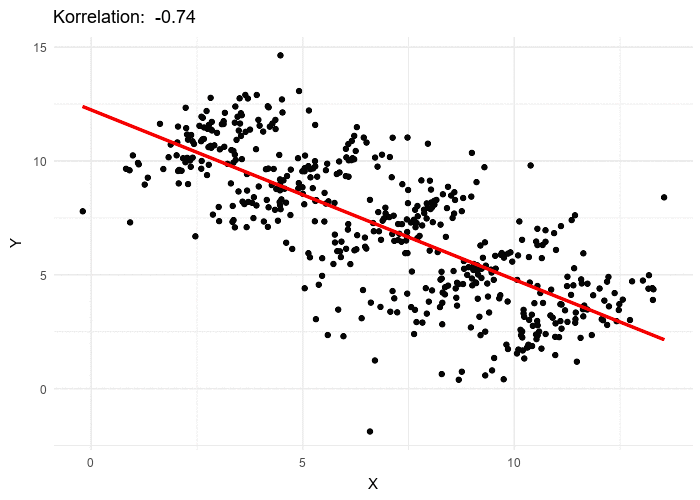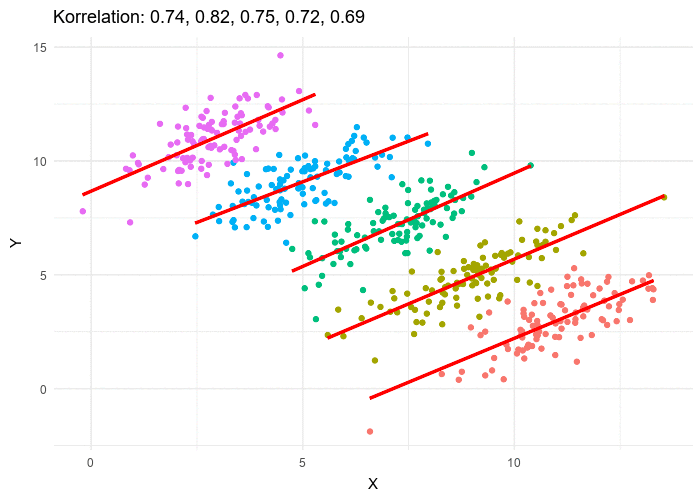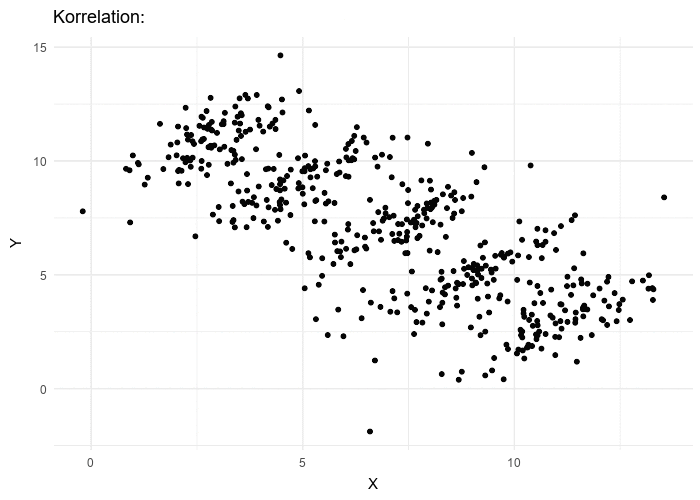
Tablo 1. X ve Y’nin Genel Bakışta Negatif Gruplandırıldığında Pozitif Korelasyonu

Simpson Vakası 1. Böbrek Taşı

Simpson'ın paradoksuyla ilgili bilinen bir örnek, böbrek taşı tedavisinde açık cerrahi ile perkütan nefrolitotomi (deriden içeri taş kırma yöntemi) arasında yapılan, tedavi yöntemlerini karşılaştıran bir çalışmadan gelmektedir. Bu çalışma, bu iki yaklaşımın başarı oranlarını, taşın büyüklüğüne göre ayrılmış şekilde özetleyen bir tabloyu içermektedir. Paradoksta küçük taşlar için açık cerrahi daha yüksek başarı oranları ile ilişkilendirilmiştir (%93.1'e karşı %86.7; Göreceli Risk (RR) = 1.07) ve büyük taşlar için de (%73.0'a karşı %68.8; RR = 1.06), buna karşın taşın çapı hesaba katılmadığında (yani, tüm verileri aldığımız toplu analizde) perkütan nefrolitotomi, açık cerrahiye göre daha etkili görünmektedir (%78.0'a karşı %82.6; RR = 0.94).

Bu şaşırtıcı durumun tersine dönmesinin arkasındaki sebep, bir hastanın hangi tedaviyi alacağının, taşların büyüklüğüne bağlı olması (karıştırıcı değişken) ile ilgilidir. Çapı 2 cm'den küçük olan böbrek taşına sahip çoğu hasta (%75.6'sı, yani 357 hastanın 270'i) perkütan nefrolitotomi almışken, çapı 2 cm'den büyük olan veya birden fazla taşa sahip olan hastaların çoğu (%76.7'si, yani 343 hastanın 263'ü) açık cerrahi almıştır (karıştırıcı değişkende dengesiz dağılım).

Simpson Vakası 2. COVID-19

Simpson'ın paradoksu, sağlık politikası kararlarının alınmasındaki etkilerini göstermek için COVID-19 döneminden daha güncel bir örnek ile de açıklanabilir. 2020 yılında, erken epidemiyolojik veriler, COVID-19'un vaka ölüm oranının İtalya'da Çin'e göre genel olarak daha yüksek olduğunu gösterdi. Ancak, bu ham analiz, yaş dağılımının (iki ülkede COVID-19 vakalarının yaş grupları arasında önemli ölçüde farklılık göstermesi nedeniyle) karıştırıcı bir faktör olduğu kanıtlandı. Yaş kategorilerine göre yapılan veri analizi, her yaş grubunda, vaka ölüm oranının aslında Çin'de İtalya'dan daha yüksek olduğunu ortaya koydu.

Simpson'ın paradoksu, klinik araştırmalarda titiz ve düşünceli istatistiksel analizlerin neden gerekli olduğunu ve sadece sezgilere dayanarak yanlış sonuçlara ne kadar kolay varılabileceğini gösteren etkileyici bir örnektir. Simpson Paradoksu bize, özellikle rastgele olmayan araştırmalardan elde edilen verilere karşı eleştirel düşünmemizi, istatistiksel olarak anlamlı her birlikteliği dikkatle yorumlamamızı, bulgu beklenmedikse iki kat dikkatli olmamızı ve karıştırıcı faktörleri dikkatle incelememizi hatırlatır. Çünkü bu tür faktörleri göz ardı etmek, tıbbi araştırma ve pratiği için yanlış ve zararlı sonuçlara yol açabilir.

Haziran 2020'de Belçika'daki farklı yaş grupları için erkekler ve kadınlar arasındaki enfeksiyon ölüm oranı (Tablo 2.) hakkındaki veriler, her yaş grubunda erkeklerin enfeksiyon ölüm oranının kadınlardan daha yüksek olduğu, ancak tüm yaş grupları bir araya getirildiğinde durumun tersine dönmesinin, istatistiklerde iyi bilinen bir olgu olduğunu ve Simpson'ın paradoksu olarak adlandırıldığını göstermektedir. Bu durumun altında yatan neden, Belçika'da yaşlı kadınların erkeklerden çok daha fazla olmasıdır. 

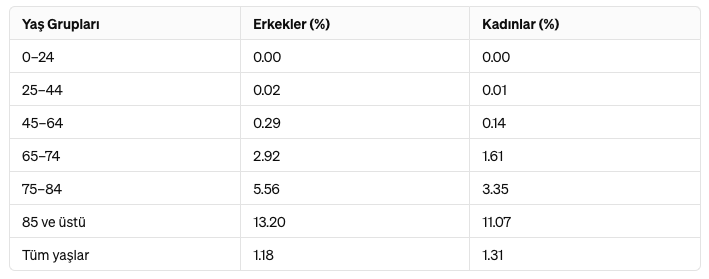
Tablo 2. Belçika’da Yaş Gruplarına Göre COVID-19’a Yakalanma Oranları

Simpson Vakası 3. Berkeley Üniversitesi Kadın / Erkek Öğrenci Kabul Oranları

1973 yılında UC Berkeley'nin lisansüstü okul başvurularında gözlemlenen durumu ele alalım. Başlangıçta, erkek adayların tüm bölümlerde kadınlara göre daha yüksek bir kabul oranına sahip olduğu görünüyordu. Bu durum erkeklere karşı olumlu bir ön yargı olduğunu öne sürüyordu. Ancak, bölüm bazında kabul oranlarının daha yakından incelenmesi, aslında kadınların daha yüksek kabul oranlarına sahip olduğunu ortaya çıkardı. Bu paradoks, toplu verilerden yanlış sonuçlar çıkarmamak için dikkatli veri analizinin önemini vurgulayan bir uyarı hikayesi olarak hizmet eder.

UC Berkeley kabul verilerini inceleyelim. İlk bakışta, genel kabul oranları erkek adayların kabul oranının daha yüksek olduğunu belirtiyor.

Erkekler: %45

Kadınlar: %30

Bu gözlem, Berkeley'nin kabul sürecinin kadınlara karşı ön yargılı olduğu sonucuna varılmasına neden olabilir. Ancak, verilere daha derinlemesine dalıp Simpson Paradoksu'nu göz önünde bulundurduğumuzda, farklı bir hikaye ortaya çıkar. Bölümsel verilerin birleştirilmesi, bölüm bazında önemli kabul oranı varyasyonlarını maskelemektedir. Bu yanıltıcı algıya katkıda bulunan faktörler şunlardır:

• Kadınların daha rekabetçi bölümlere başvurma eğilimi, genel kabul oranlarını düşürür.
• Erkeklerin daha az rekabetçi bölümlere yönelme eğilimi, kabul oranlarını artırır.

Her bölümün özel kabul oranlarını hesaba katan daha nüanslı bir analiz, daha net bir tablo sunar. Bu bağlamda, kadınlar çoğu bölümde erkeklere karşı hafif bir avantaja sahiptir, başlangıçtaki ön yargılı yorumu sorgular.

Sonuç olarak Simpson Paradoksu, veri analizi ve istatistiksel çıkarımlarda karşılaşılan karmaşıklıkları ve potansiyel yanılgıları vurgulayarak, özellikle tıbbi araştırmalar ve politika yapımında dikkatli bir yaklaşımın önemini ortaya koymaktadır.